コリオリの力
我々自身はまったく意識していないが、我々は地球の自転と共に、もの凄い速度で空間を移動しており、その力（慣性力）を絶えず受けているわけである。その所持する物体も同様だが、その物体は我々の手を離れた途端に我々の体とは無関係に、地球の自転の力を個別に受け、物体が投棄されたその速度と地球の自転の力との両方の力を受ける結果、極方向に投棄された物体の進行方向は力の平行四辺形によって右に曲がるわけである。
（以下引用）
地球の自転のもう一つの証拠は、地球では運動している物体に対してコリオリの力（転向力）というものが働いて、北半球では運動している物体が進行方向に対して右へ右へと曲げられていく（南半球では左へ左へと曲げられていく）という現象である。これも、理解が少し難しい。
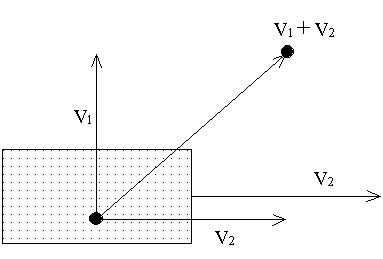
いまＶ2という速度（速さと向きを考えた量）で動いている電車の中から、電車に対してＶ1という速さでボールを投げる（本当にやってはいけない）。ここでは簡単にするために、電車の速度に対して直角方向に投げているが、本当はどの向きにボールを投げても、Ｖ1とV2が作る平行四辺形の対角線の向きに斜めに飛んでいく（地上から見た場合）。これは力の平行四辺形と同じである。
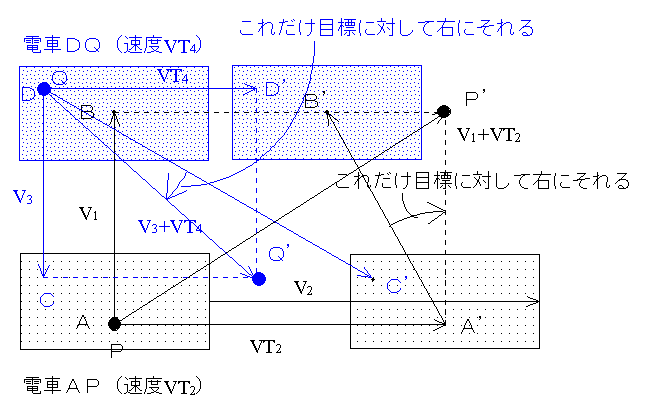
ここで、平行して同じ向きに同じ速さで等速直線運動をしている2台の電車を考える。下図の下の電車の速度VT2＞上の電車の速度VT4とする。いま、下の電車のＡから上の電車のＢに向けてボールＰを投げる。ボールはつねにＡの真ん前を飛んでいき、ある時間後にはＰ’に到達する。しかし、目標であったＢはまだＢ’の位置にまでしか来ていない。ここで、電車の姿やまわりの景色はまったく見えず、電車が動いているときの振動もなく、目標のBだけしか見えないとすると、ボールＰを投げた人にとっては、なぜか目標であるＢ（Ｂ’に移動している）にボールが当たらず、ボールは目標の右に自然にそれてしまったように思えるだろう。
逆に、上の電車Ｄから下の電車Ｃに向かってボールを投げても、Ｄにいる人にとってはボールは目標であるＣ（Ｃ’に移動している）には当たらず、同じように目標に対して右にそれることがわかる。
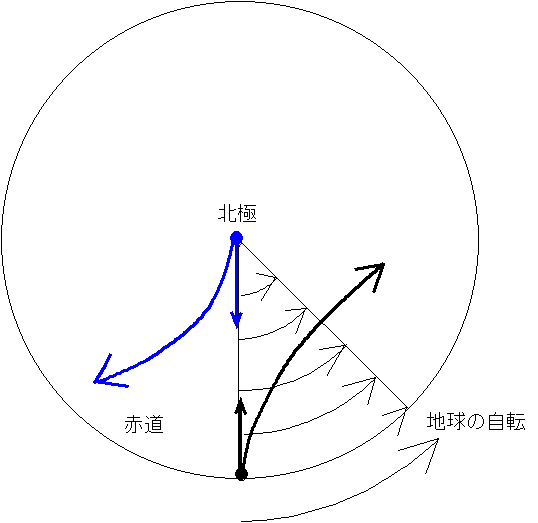
地球を下の図のような円盤として考える。地球の自転による回転の距離の大きさ（つまり速さ）は赤道で最大、北極に向かってだんだん小さくなり、北極で最小（０）になる。だから上の図のように、赤道から北極向かってボールを投げようが、北極から赤道に向かってボールを投げようが、いずれにしても目標に向かってまっすぐには飛んでいかず、なぜか右へ右へと曲がっていってしまうことになる。
このように、回転している地球の上では、物体の進行方向を曲げようとする力が働いているように見えるので、これをコリオリの力（転向力）という。でも、これは“本当の力”ではなく、どのような立場で運動を見ているか、その立場の違いで生ずる“見かけの力”なのである。ここではそれについては深入りしない。コリオリの力の大きさの見積もりは下を参照。
コリオリ：フランスの物理学者（1792年～1843年）。
ともかく、実際地球上で、例えば運動場でボールを思いっきり投げても、そのボールが必ずすべて右へ右へと曲げられていくことはない。もし、日常生活でもコリオリの力の影響が見えるなら、古代の人も地球の自転に気が付いていただろう。コリオリの力は、気象現象（高気圧・低気圧の風など）の大規模なスケールでないと、その影響が見えてこないのである。
低気圧の渦が、北半球では必ず左巻き、南半球では必ず右巻きになるのは、コリオリの力のせいである。これは今日では、気象衛星の写真を見ると一目瞭然であり、これこそが地球の自転の証拠なのである。高気圧・低気圧などの風の吹き方はこちらを参照。どのような場合にコリオリの力の影響が現れて、どのような場合は無視できるかは下を参照。